Numerical Schemes, Discretization Schemes for OpenFOAM®
For numerical analysis, one deals with partial differential equations. These equations are solved in time and space. Performing numerical simulations by using OpenFOAM®, one has to choose a discretization scheme for each partial differential term from a large list of numerical schemes. However, each discretization method has its numerical behavior. Thus, depending on the scheme in use, higher accuracy in terms of quantity representation (physically more correct) or numerical stability can be achieved. The following two examples allow one to analyze different OpenFOAM® schemes related to their accuracy and stability for different mesh types (cell shapes), mesh densities, and OpenFOAM® versions. The »OpenFOAM® Scheme Comparison« includes the popular analyzer built by Tobias Holzmann in the year 2013. The new added »OpenFOAM® Scheme Validation« compares the different numerical schemes against measurement data and was invented in the year 2020. Thanks to Arjun Y. for the hint.
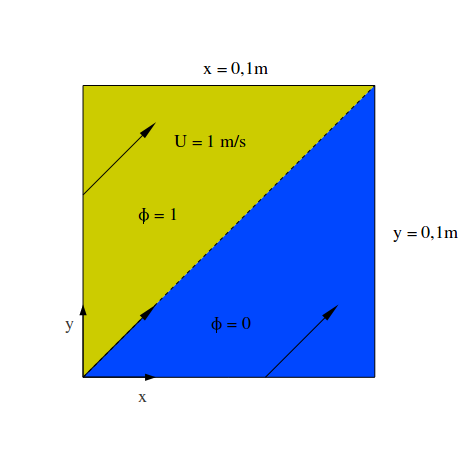
Convective Scalar Transport
Compare different convective schemes against each other on different meshes and OpenFOAM® versions for a convective scalar transport case
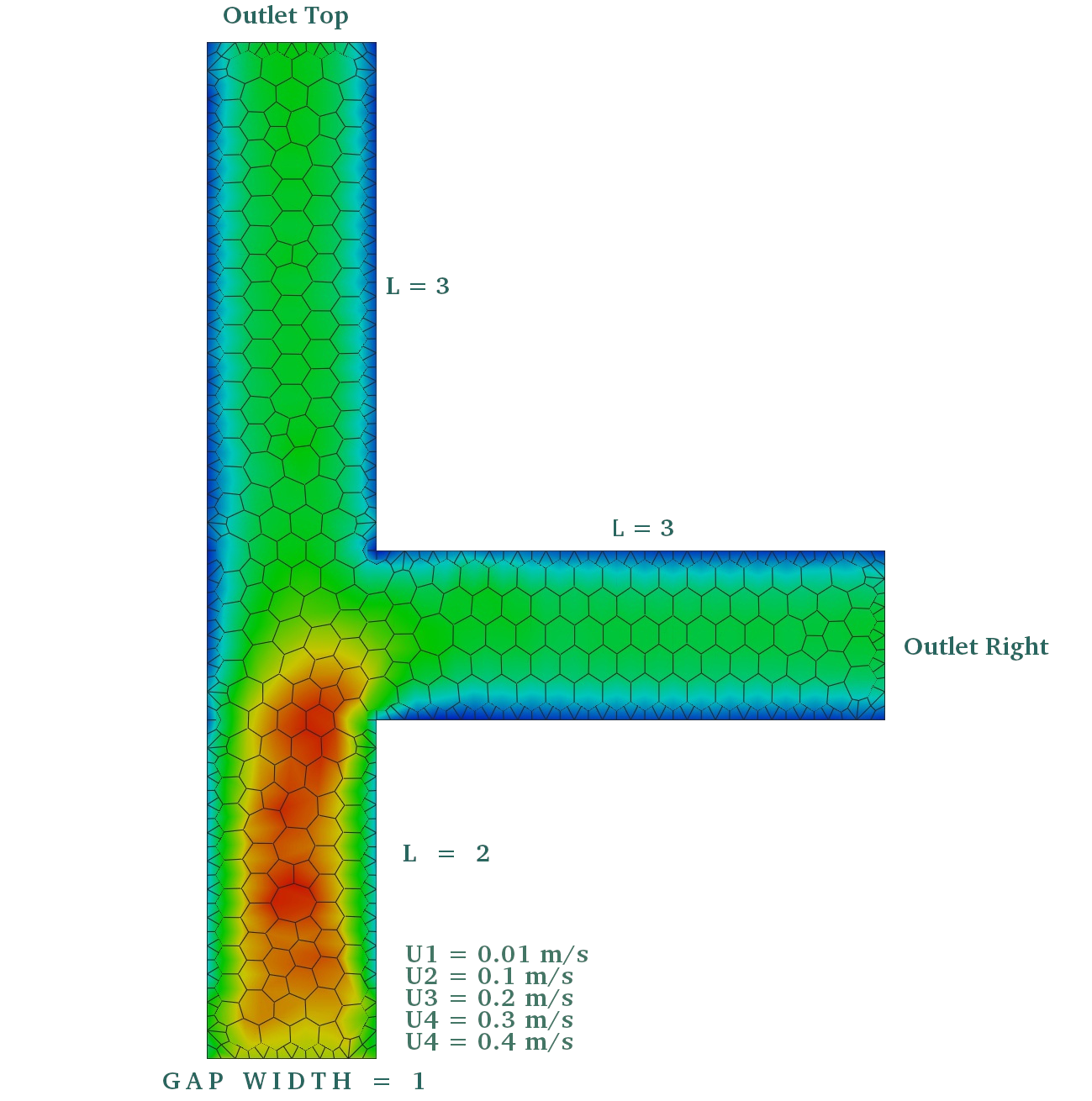
Convective-Diffusion Transport
Analyze and compare different convective schemes against measurement data in a simple T-shaped pipe