Convective-Schemes Analysis in Convective-Diffusion Problems
The following analysis investigates into the convective schemes one can use in OpenFOAM®. As everybody knows, a numerical scheme has to be stable and accurate to get the linear solver working properly and to get reasonable results. The following analyzer investigates into a T-shaped pipe in which the velocity at the inlet is increased five times to achieve different Reynolds numbers (laminar). The pressure at both outlets is set to 0 Pa/kg/m³. The case can be understood as follows. For very low Reynolds numbers, there is a flow separation which results in an equal split of the mass flow rate through outlet 1 (top) and outlet 2 (right one). The higher the velocity gets, the more mass is leaving outlet 1 at the top based on the inertia of the fluid.
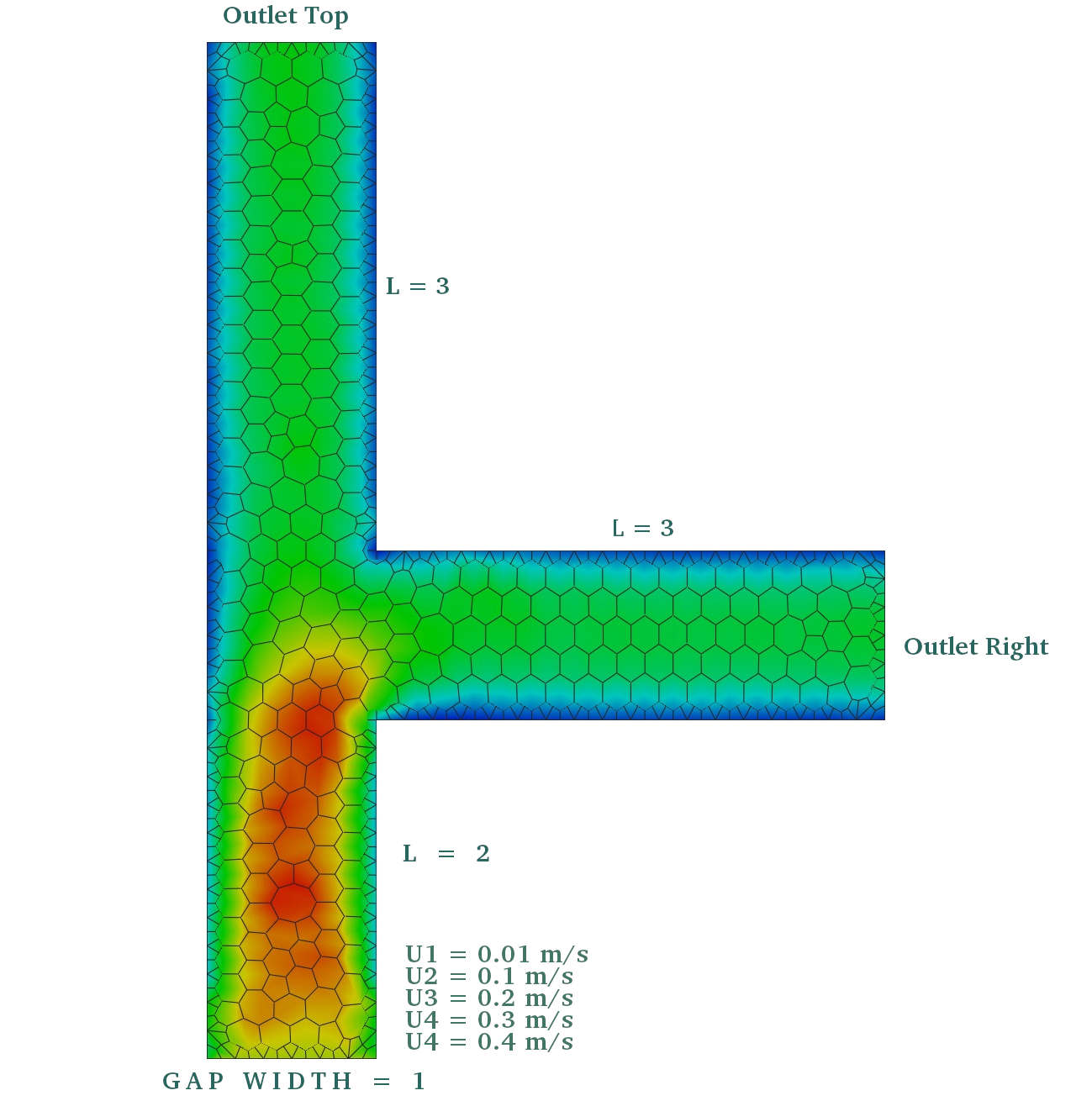
This case is more complex compared to the »Scalar Transport« analysis as the pressure-momentum coupling is solved. However, as momentum diffusion occurs, the gradients are smoothed based on the laplacian term which will support the stability of the numerical calculation. The diffusion coefficient is set to a value of 0.001 Pas. It represents the dynamic viscosity of the fluid in use and is high viscous compared to air or water.
The new validation case is based on Arjun Y. `s inspiration and the corporation
The numerical investigation presented below compares different convective discretization schemes of OpenFOAM® against measurement data (it is an ANSYS Fluent test case). In comparison to the »Scalar Transport« investigation, different mesh types (hexahedral, tetrahedral, and polyhedral) and different mesh densities are investigated and can be compared against each other as well as against the measurement data and different OpenFOAM® versions.
Warning: Undefined array key 1 in /var/www/web610/html/holzmanncfd/modules/mod_downloader/tmpl/default.php on line 19
Warning: Undefined array key 1 in /var/www/web610/html/holzmanncfd/modules/mod_downloader/tmpl/default.php on line 19
Important notice: All simulations are done with the same control settings. Hence, it can happen that some schemes will blow up although the scheme would produce reasonable results if one chooses other relaxation factors or incorporate other numerical stabilization criteria. The analysis is performed using the incompressible (density is constant) pressure-based solver named »simpleFoam«.
Structured Mesh



Unstructured Mesh (Tetrahedral)
Arbitrary face-angles



Structured Mesh (Polyhedral)
Arbitrary face-angles




